All permutations of an array

• 04 september 2021
• backtracking,
• psds

Hi! Today I would go over on how I approach the problem of finding all possible permutations of an array.

input = [1, 2, 3]
output = [
    [1, 2, 3],
    [1, 3, 2],
    [2, 1, 3],
    [2, 3, 1],
    [3, 1, 2],
    [3, 2, 1]
]

So you see the task is to enumerate the input array in all combinations and return them.

basic concept #

This can be solved if you can visualize it as fixing the position of a number and then generating all other variants using a recursive call. Let's understand it in a more pictorial manner.

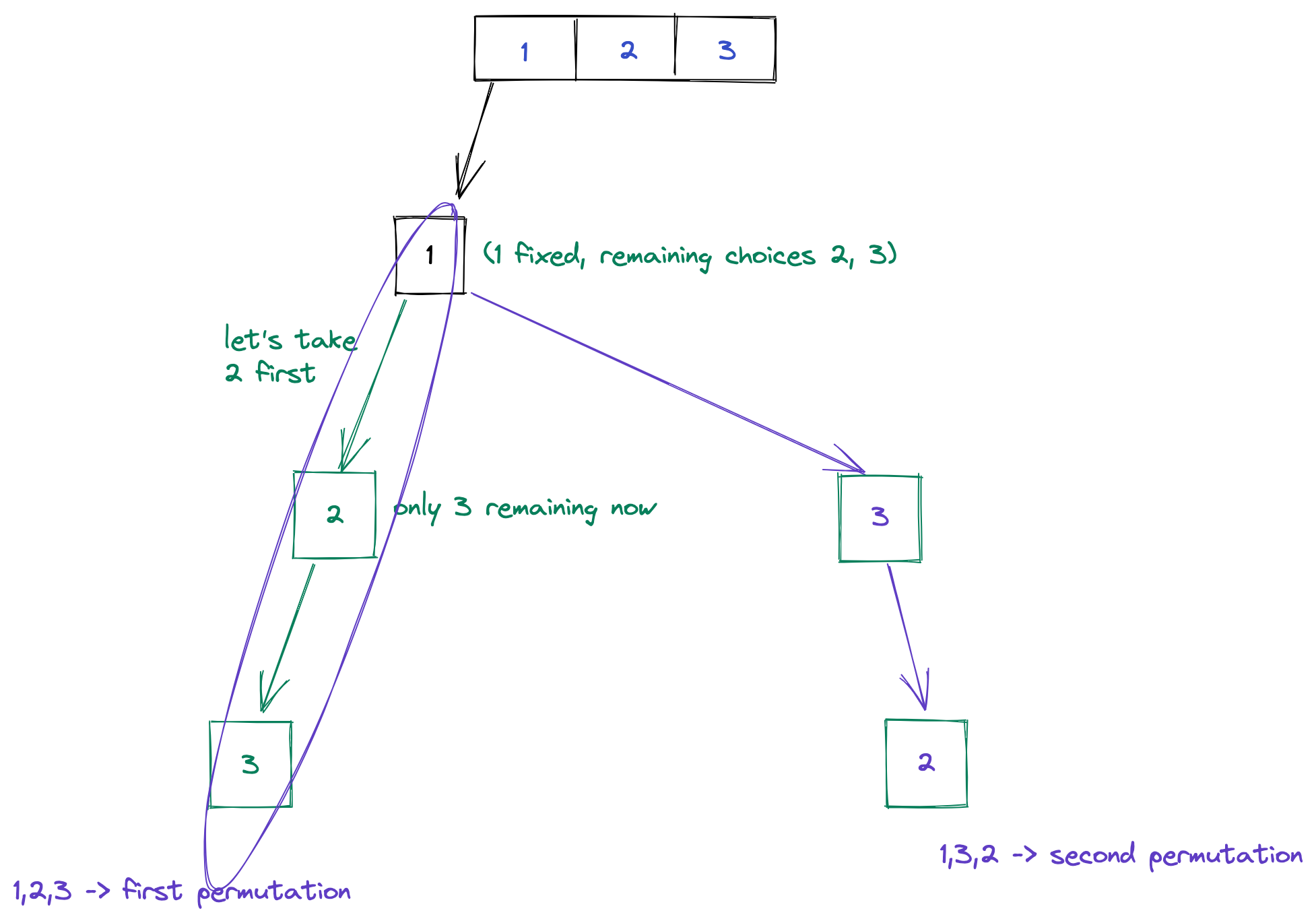
Similarly we can trace the next permutations by starting with 2 and then with 3

algorithm #

• start with 2 arrays
  • one is the input array
  • second is the array in which we'll add each permutation as we encounter
• from the input array, choose 1 number and fix it
  • do that till input array is not empty
  • once the input array is empty, we've chosen all the elements and we can store that result

code #

const permute = (input = [], permutation = []) => {
  if (input.length === 0) return [permutation]; // this will be one of the result

  // choose each number in a loop
  return input.reduce((allPermutations, current) => {
    // reduce the input by removing the current element
    // as we'll fix it by putting it in `permutation` array
    const rest = input.filter((n) => n != current);
    return [
      ...allPermutations,
      // fixing our choice in the 2nd arg
      // by concatenationg current with permutation
      ...permute(rest, [...permutation, current]),
    ];
  }, []);
};

The solution looks so tiny, let's dissect it line by line. The inputs of the function are nothing but the input and an array that'll store our choice as we go deeper into the recursion tree. Taking the example of the above diagram for the 1, 2, 3

(input = [1, 2, 3]), (permutation = []);
// first recursion will be called with
(input = [2, 3]), (permutation = [1]);
// as we're creating a rest array with every element except the `current` which is 1
(input = [3]), (permutation = [1, 2]);
// next recursion
(input = []), (permutation = [1, 2, 3]);
// at this point we hit our base condition
// and we return [[1, 2, 3]], creating a double array
// so that ... does not disturb and open the permutation array
// next we come back and use 3 instead of 2
(input = [2]), (permutation = [1, 3]);
// next recursion
(input = []), (permutation = [1, 3, 2]);
// and so on...

practise #

You can practise this question on leetcode

• previous: Calling gRPC services from UI!
• next: Simplify Paths