Asteroid Collision
Hi! Today I'll go through the problem asteroid collision and solve it with you!
problem #
You're given an array of numbers, some positive and some negative. Each number signifies how big is the asteroid, bigger the absolute number bigger the size.
- positive numbers mean they move right ->
- negative numbers mean they move left <-
Asteroids moving towards each other will collide and the bigger one will win with smaller one being destroyed. If both are of the same size then both will get destroyed.
You need to return the asteroids that will be left after the collision 💥💥💥
concept #
I'll use the two pointer approach.
- left pointer
- right pointer
I'll keep on checking if the adjacent asteroids are colliding, and keep incrementing/decrementing the pointers till the entire array of asteroids are exhausted. This can be done either recursively or iteratively.
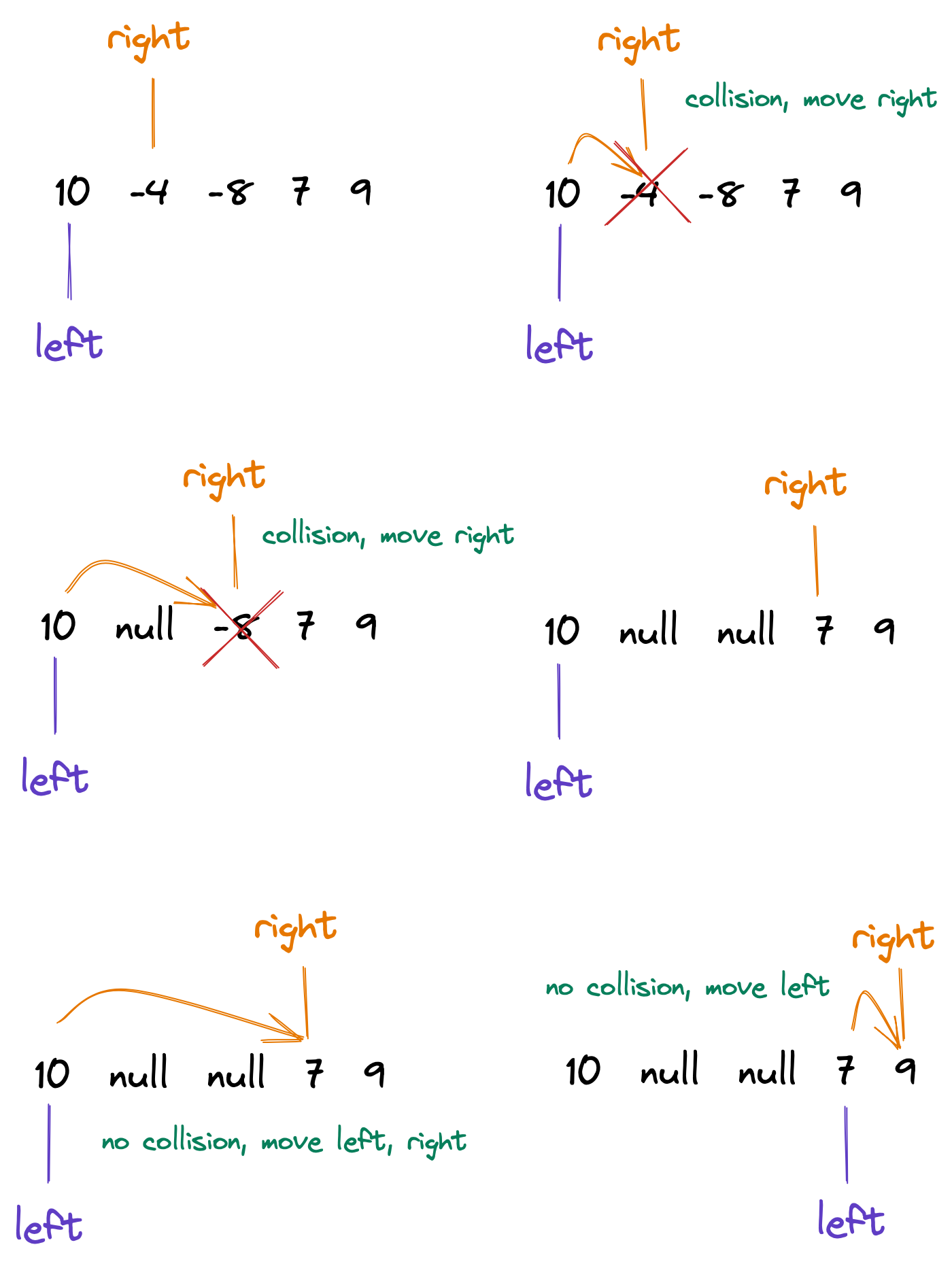
Let's see for input [10, -4, -8, 7, 9], how the above approach works.
code #
Let's start by defining the pointers and the main loop as below.
var asteroidCollision = function (asteroids) {
let left = 0;
let right = 1;
const willCollide = () => {}; // will return a boolean
const adjustLeft = () => {}; // TODO
while (left < asteroids.length && right < asteroids.length) {
const isColliding = willCollide();
const absLeft = Math.abs(asteroids[left]);
const absRight = Math.abs(asteroids[right]);
if (isColliding) {
if (absLeft > absRight) {
asteroids[right] = null;
right++;
}
if (absLeft < absRight) {
asteroids[left] = null;
adjustLeft();
}
if (absLeft === absRight) {
asteroids[right] = null;
asteroids[left] = null;
right++;
adjustLeft();
}
} else {
// not colliding, simply move the pointers
left = right;
right++;
}
}
return asteroids.filter(Boolean);
};In the above solution, we've two pointers left and right starting at 0 and 1 respectively.
The main loop will go on till any of the pointers go outside the bound of input array. So far so cool.
algorithm #
- on every loop, check if the asteroids present on left and right will collide or not.
- I'll define the function
willCollidein just a moment, but for now it returns a boolean - simple case: if the asteroids don't collide, just move the pointers
- and if the asteroids are colliding, there are three conditions that need to be handled
- if left is bigger
- then right one goes boom 💥
- move the right pointer further along
- if the right is bigger
- make the left one 💥
- adjust the left pointer (we'll come to this in just a min)
- if both are of same size
- both go boooom 💥
- move the right pointer and adjust left
- if left is bigger
- finally, ignore all the
nullvalues and return the remaining asteroids for the answer
willCollide #
- out of all the ways possible the two asteroids will only collide if the left is going right -> and the right is going <-
- you might be tempted to keep a variable that checks if the sign changes from the last asteroid and if it does than baamm!
- but no, if the left asteroid is going left <-, and the right asteroid is going right ->, then the two will never collide
So coding the above in a sweet function.
const willCollide = () => {
if (asteroids[left] > -1 && asteroids[right] < 0) return true;
return false;
};adjustLeft #
- this is a fun bit, where we'll land in if the left asteroid gets destroyed.
- we've two options here
- either go leftwards and find an existing asteroid
- or if no asteroid is left, then make the right asteroid the left
- and increment the right pointer
const adjustLeft = () => {
// starting one less than the right (going leftwards)
let start = right - 1;
while (start >= 0) {
// as soon as we find a health asteroid, assign it to left pointer
// and immediately return
if (asteroids[start] !== null) {
left = start;
return;
}
start--;
}
// if the control reaches here then it means all the asteroids to the left
// of right pointer are dead, make right one the left
left = right;
right++;
};practise #
You can practise this question on leetcode. As a fun challenge, try to do this recursively and shout-out on Twitter?